2022. 1. 29. 12:51ㆍ책/누구나 자료 구조와 알고리즘
빅 오는 분명 훌륭한 판단 지표이긴 하나 유일한 지표는 아니다.
같은 효율성을 갖는다고 해도 실제로는 어느 하나가 더 빠른 경우가 많기 때문이다.
효율성이 같아 보이는 두 알고리즘을 뭐가 더 빠른지 어떻게 골라낼까?
5.1 선택 정렬(selection sort)
매 패스스루마다 가장 작은 값을 찾아서 맨 앞으로 빼내면서 정렬하는 알고리즘
아래 예시는 총 12단계가 소요된다
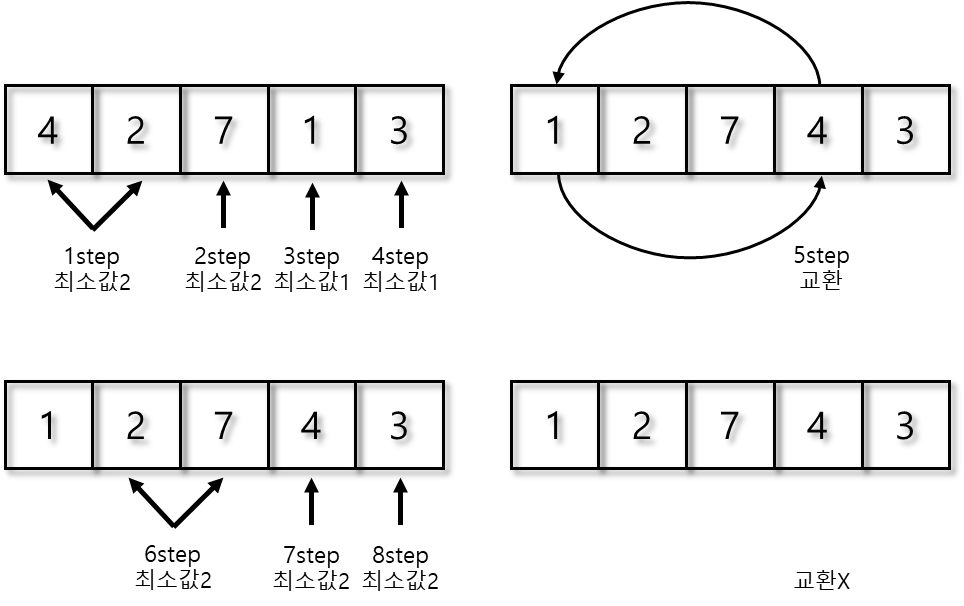
5.2 선택 정렬의 효율성 ( O(N²) )
선택 정렬은 비교
function selectionSort(arr: number[]) {
for (let i=0; i<arr.length; i++) {
let lowestIndex = i;
for (let j=i+1; j<arr.length; j++) {
if (arr[j] < arr[lowestIndex]) lowestIndex = j;
}
[arr[i], arr[lowestIndex]] = [arr[lowestIndex], arr[i]];
}
return arr
}비교와 교환 두 단계를 포함하며, 각 패스스루당 소요 단계는 아래와 같다
(최악의 시나리오 기준으로, 교환이 매 패스스루마다 무조건 1번씩 일어나게 될 것이다)
- 비교 : ( N-1 ) + ( N-2 ) + ( N-3 ) + ... + 1 = N(N-1)/2
- 교환 : 1 + 1 + 1 + ... + 1 = N-1
☞ 총 (N-1)(N/2+1) 단계
즉, 근사적으로 (N²/2) 단계가 소요되며 빅 오 표기법으론 O(N²)가 된다.
???
왜 O(N²/2)가 아닐까??
5.3 상수 무시하기
분명 버블 정렬하고 거의 2배나 차이나는데 왜 표기법은 같을까?
사실 '빅 오 표기법은 상수를 무시한다'
즉, 빅 오 표기법은 몇 차 함수로 그려지냐를 나타낼 뿐 세세한 단계까지 다 나타내는 지표는 아니다

위 함수처럼 기울기가 두배든 열배든 이차 함수라는 점에선 똑같은데,
빅 오 표기법도 쉽게 말해 몇 차 함수인지만 나타낼 뿐이다 (실제 단계가 100배 넘게 차이가 나도 알 바 아님 ㅅㄱ)
5.4 빅 오 카테고리
빅 오 표기법은 일반적인 카테고리의 알고리즘 속도만 고려한다.
위 얘기를 다시하는 꼴이지만 결국 몇 차 함수인지만 따질 뿐
5.5 마무리
지금까지 두 알고리즘 효율성을 비교할 때 최악의 시나리오를 기준으로 했다
그런데 사실 실제로 일어나는 시나리오는 평균 시나리오다
이건 6장에서 ㄱㄱ
'책 > 누구나 자료 구조와 알고리즘' 카테고리의 다른 글
| [17장] 트라이(trie)해 보는 것도 나쁘지 않다 (0) | 2022.03.06 |
|---|---|
| [6장] 긍정적인 시나리오 최적화 (0) | 2022.02.14 |
| [4장] 빅 오로 코드 속도 올리기 (0) | 2022.01.26 |
| [3장] 빅 오 표기법 (0) | 2022.01.26 |
| [2장] 알고리즘이 중요한 까닭 (0) | 2022.01.24 |